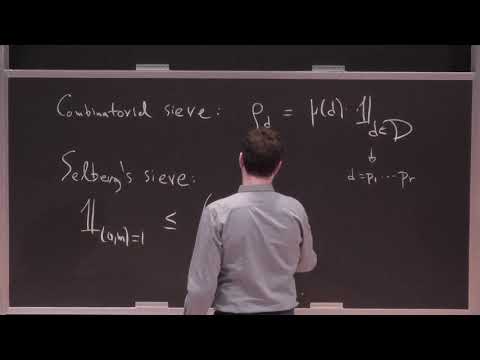Among the mathematical theorems, conjectures and hypotheses that scientists have been working on for more than a century, there are still at least ten famous problems (theorems, conjectures, hypotheses) that remain unsolved and attract the center of the international mathematical community on their solution.

One of these problems, the “RJ Duffin and AC Schaeffer” Theorem, which has been troubling the Mathematical Theory of Numbers for 78 years, was solved in 2019 by Greek Dimitris Koukoulopoulos, Associate Professor at the University of Montreal, and his partner James Maynard from Oxford.

The “Duffin-Schaeffer” Theorem, which was formulated by the two mathematicians in an article in 1941 and remained unsolved until about 1990, although some small results were found to its answer, remained unsolved until 2019.

The two mathematicians, Koukoulopoulos and Maynard, in fact, have introduced a detail that says that if we ban some denominators even a sparse subset of them, some numbers may never be reached.

The young Greek mathematician does not hide his delight at the task of solving one of the central problems in the field of number theory after 78 years – it is called a “diophantine approach”, in honor of Diophantus of Alexandria, one of the ancient Greeks mathematicians, and has to do with fractional numbers approximations.

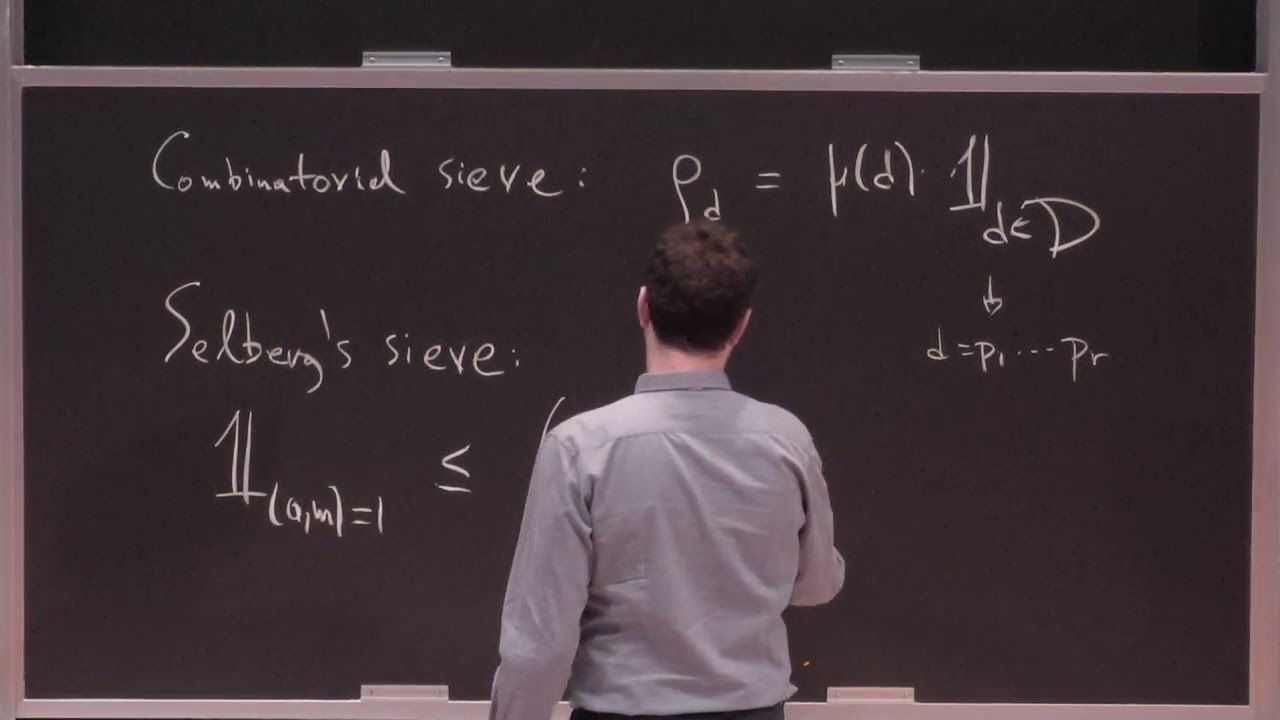
Proof of the Theorem, according to Mr. Koukoulakis, does not mean, in relation to other sciences, any kind of application to life, as he cannot imagine how this particular theorem could be applied in one way or another, because apart from everything else, it is a metrical theorem. “I don’t know if there will be any concrete application. In theoretical mathematics, it would be nice to see your work applied in real life but the nature of theoretical mathematics is such that applying ideas can take many years until something is done or even an indirect contribution is made. ”

He adds that in theoretical mathematics, as in most theoretical sciences, one works intensively even for the rest of his life to understand and solve a question without necessarily knowing whether it will have real-world implications. However, he points out that funding for research in theoretical mathematics is fundamental because in ways we cannot understand, it also affects research in applied mathematics, engineering and physics.

To reinforce what he said, he added, speaking to APE-MPE, a doctrinal description from the story of a famous British mathematician, Godfrey Harold Hardy, known for his contributions to number theory and analysis and also for the dissertation “A Mathematician’s Apology”. The mathematician noted that he was satisfied that he was working in a field that had no application in real life because he did not want his work to be used in war.

Unfortunately, however, – says Mr. Koukoulopoulos – what the famous mathematician said was completely disproved because after several years when IT and communications were developed there was a great need for the secure transmission of signals. And signal encryption is often done using ideas from number theory. “That’s why I’m telling you it’s hard to predict where your achievement can end up. And Hardy was wrong, he denied it and today if he lived he might be very disappointed with the evolution. ”

Dimitris Koukoulopoulos graduated from the 2nd High-School of Kozani and then entered the Aristotle University of Thessaloniki: School of Mathematics. In the last year of his studies, he applied to various US universities, as that was where he had always intended to study. He chose to pursue a doctorate directly at the University of Illinois, due to its very good team in Analytical Number Theory, which is his research field.

In 2012, at the age of just 28, he was hired as an assistant professor at the University of Montreal and today, at the age of 35, he is an adjunct professor at the same university.

As to the plans the future may hold for someone who has accomplished so many things in such a short time, he responds disarmingly that “I have no plans”, but adds that after the theorem was resolved “a long period of my life, which was opened a few years ago, came to an end. I am getting ready for the new academic year, and I will devote myself entirely to my students and Ph.D. candidates with new things on the agenda. “